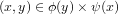 ,
,
Consider a social dilemma where public-goods contributions are perfect substitutes. This corresponds to Evolutionary Stability, Co-operation and Hamilton's
Rule
, Ingela Alger and Jörgen Weibull, section 4.4.1.
Let player strategies x, y be strategy profiles in X, the set of strategies in a symmetric personal-fitness game G = (X, π) fully defined in sec. 2.1 of the paper. Let behaviour rules φ, ψ be functions of φ : X → X assigning a non-empty subset of the strategy space as a response to the other player's strategy. Then, given strategies
,
a pair of real-valued traits α and β is mutually compatible when satisfying
.
In the first equation, α is the first player's weight assigned to the other player's utility. In the second case, this is β. In words, a positive α or β expresses altruism; a negative value, spite; and a zero value, selfishness. Next, let x*(α, β) be the unique strategy of an α-altruist when matched to a β-altruist. The increase in fitness is then
.
Finally, letting H be the gradient of evolutionary stability (as defined in section 2.2 of the paper), the evolution gradient over α, the incumbent degree of altruism, and α′, the mutant degree, where subscripts are derivatives, is defined as
.
Consider the the additive contribution case,
.
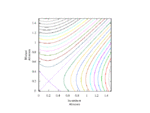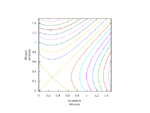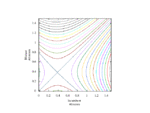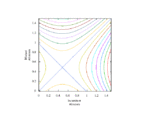
Fixing τ = 0.5 (strategic substitutes), relatedness r = 0.5, and cost c = 1, this produces the following static plots of function H, where v is linear, over intervals of α and β.
Full-size | eps

Full-size | eps

Full-size | eps

Now, fixing cost c = 1 and relatedness r = 0.5, fluctuate τ monotonically-increasing over [0, 1] with fixed τ = 1.0 (strategic independence).
Full-size
Full-size
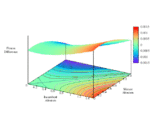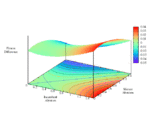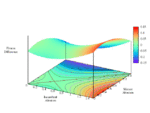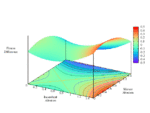
Full-size
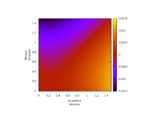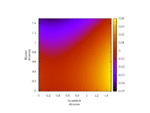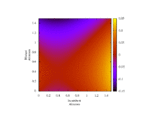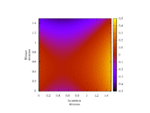
Lastly, fixing cost c = 1 and τ = 0.5 (strategic substitutes), fluctuate r monotonically-increasing over [0, 1].
Full-size
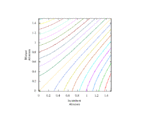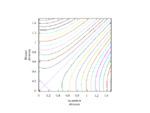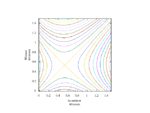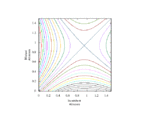
Full-size
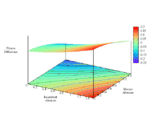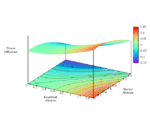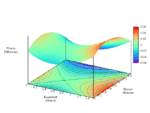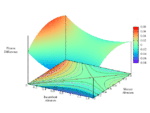
Full-size
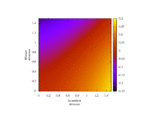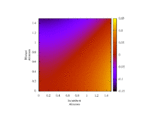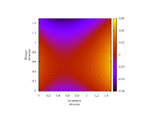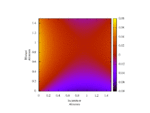
← Back to index. Kristaps Dzonsons, $Date: 2011/02/03 13:48:55 $