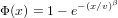 , where β = v = 1, as seed to the aggregation
function
, where β = v = 1, as seed to the aggregation
function 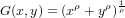 .
This applies to § 5.3,
.
This applies to § 5.3, Weibull, of
Extreme Values, Invariance, and Choice Probabilities(which uses the ccdf). Using the following cdf,
First, apply the Weibull distribution, 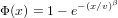 , where β = v = 1, as seed to the aggregation
function
, where β = v = 1, as seed to the aggregation
function 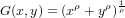 .
This applies to § 5.3,
.
This applies to § 5.3, Weibull
, of Extreme Values, Invariance, and Choice Probabilities
(which uses the ccdf).
Using the following cdf,
where a = b = 1, we let
Differentiate twice to find the density function of the cdf, producing
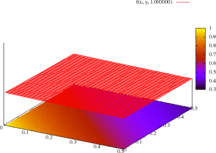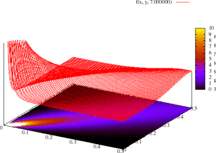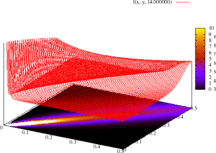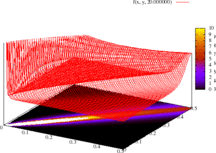
Function f(x, y, ρ) produces the following plots at ρ = 2. The first plots the function value at the given co-ordinate points, the second plots line contours, and the third renders the contours over a colour spectrum. Notice how the plot clusters along the diagonal.
These plots differ from other extreme-value examples because of the function's slope: to create meaningful output, the z-range has been significantly cropped.
Full-size

Full-size

Full-size

The following are animations of a monotonically-increasing value of ρ = 1, ..., 20 for f(x, y, ρ).
Full-size
Full-size

Full-size

Below is a listing of available stills in EPS (full-colour and monochrome Encapsulated PostScript) for easy type-setting and PNG (full-colour Portable Network Graphics) for multimedia. They're arranged by type (three-dimensional plot, contour lines, spectral contours) and variable ρ for function f(x, y, ρ).
← Back to index. Kristaps Dzonsons, $Date: 2011/03/08 11:13:50 $